2019年普通高等学校招生全国统一考试（全国 II卷）
理科数学
1、选择题
1. 设集合
，
，则
答案：
A
解答：
或
，
，∴
.
2. 设
,则在复平面内
对应的点坐落于（ ）
A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案：
C
分析：
，对应的点坐标为
,故选C.
3．已知，
，
，则
（ ）
A.
B.
C.
D.
答案：
C
解答：
∵
，
∴
，解得，
，
∴.
4．2019年1月3日嫦娥四号探测器成功达成人类历史上初次月球背面软着陆，国内航天事业获得又一重大收获。达成月球背面软着路需要解决的一个重点技术问题是地面与探测器的通讯联系。为解决这个问题，发射了嫦娥四号中继星“鹊桥”，鹊桥沿着围绕地球月拉格朗日
点的轨道运行，点是平衡点，坐落于地月连线的延长线上。设地球的水平为
，月球水平为
，地月距离为
，
点到月球的距离为，依据牛顿运动定律和万有引力定律，满足方程
。设
。因为
的值非常小，因此在近似计算中，则的近似值为（ ）
A．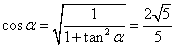
B．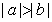
C．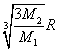
D．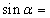
答案：
D
解答：
所以有
化简可得
，可得。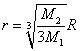
5. 演讲比赛共有9位评委分别给出某位选手的原始评分，评定该选手的成绩时，从9个原始评分中去掉1个最高分、1个最低分，得到7个有效评分。7个有效评分与9个原始评分相比，不变的数字特点是（ ）
中位数
平均数
方差
D．极差
答案：
A
解答：
因为共9个评委，将评委所给分数从小到大排列，中位数是第5个，假设为，去掉一头一尾的最低和最高分后，中位数还是，所以不变的是数字特点是中位数。其它的数字特点都会改变。
6. 若，则（ ）
A.
B.
C.
D.
答案：
C
解答：
由函数
在上是增函数，且，可得
，即.
7. 设为两个平面，则的充要条件是
A. 内有无数条直线与
平行
B. 内有两条相交直线与平行
C. 平行于同一条直线
D. 垂直于同一平面
答案：
B
分析：
依据面面平行的断定定理易得答案.选B.
8. 若抛物线的焦点是椭圆
的一个焦点，则（ ）
A.2
B.3
C.4
D.8
答案：
D
解答：
抛物线的焦点是
，椭圆的焦点是，
∴
，∴
.
9. 下列函数中，以
为周期且在区间单调递增的是（ ）
答案：
A
解答：
对于A,函数的周期,在区间单调递增,符合题意；
对于B,函数的周期,在区间单调递减,不符合题意；
对于C，函数，周期,不符合题意；
对于D,函数的周期,不符合题意.
10. 已知
，
，则（ ）
A. 
B. 
C.
D.
答案：
B
分析：
，
，
则，所以，
所以.
